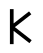Painting Sad/Happy Pictures

Continuing with our Voices in the Park art work, based on these two illustrations -

- we've been preparing and painting our own sad-happy pairs.

See a slideshow of us working here:

Maryam's Claim

In 4G we've been looking at some squares we divided up, asking what fraction each part is. It's easy to see the eighths in this one, but what about the triangles on the left?

Then Maryam made her claim: "As long as it's the midpoint, it doesn't matter how you split the triangle; it will always be half." It was a really interesting mathematical claim, and one we had to really think about - Mr Gregg too!

Most people didn't agree - the triangles on the left do not look like they have the same area.

We tried it on Geogebra. Still most people thought the two triangles had different areas.

John Golden suggested on Twitter that we see how you can get same-area triangles (if you start with the same "base"):

>


We also had a look at this:

This convinced a lot of us that Maryam's claim was true.

But Miguel was still not convinced:
"Technology isn't perfect. Is that really a proof?"

Dan Finkel suggested on Twitter that we change our triangle into a parallelogram and it will make it easier to see the truth:


We had a really good discussion about this, and quite a few people tried to persuade Miguel. Well done Miguel for getting us really thinking! There were all sorts of really good arguments to show how the two parts of the triangle in fact have equal areas.

After this we wrote down what we thought about it all:

Rhea's Painting

Rhea showed us a lovely painting that she's been doing on Wednesday afternoon. 

It's a watercolour painting. Hopefully she's going to be doing lots more!

Voices in the Park

What had been a black and dirty street was now a neat and golden street.
What had been old boring pictures were now dancing and laughing people.
What had been a penniless Father Christmas begging was now a jolly dancing Father Christmas.
What had been an old damp lamp post was now a fantastic beautiful flower post.

Voices in the Park

He had exhausted his plan and he was still a bit sad. Before the Santa was so sad sitting down on the floor and then after he was dancing all around. First the portraits were all sad and after they were dancing and they are all happy when they are dancing. In the day it's  all unhappy and at night it is all happy. In the day the trees are bent and at night they are alive. And in the day there is the two hotels that are all unhappy and at night it is all colourful there's little symbols in it.

Voices in the Park

He was sad and depressed now he was bright and happy. What had been bent dull trees were now flowering and standing straight.  The beggar was now dancing ballet everywhere. The old lamp post was now a beautiful flower. The dirty street was now clean and a nice place to be.
                               

Voices in the Park

At first the person dressed as Santa was a poor and a sad beggar but now he was a cheerful, happy ballet dancer. The old, plain lamp-post was now a pretty, flower-shaped lamp-post.
What had been two, plain paintings were now real people dancing gracefully and joyfully. What had been a dull, broken wall with a broken heart changed to a bright, sturdy wall with a red, nice heart. The boring, grey flats were now colourful flats with different shaped windows.

Voices in the Park

We're reading Voices in the Park by Anthony Browne at the moment, taking our time to look really carefully at the illustrations.

For instance these two pictures:

before

after

We've been writing about the change:

4B have also written blog posts about the changes - see separate posts.

 

We're also creating our own pictures starting from our sketches outside, that show a "sad" before and a "happy" after:

 

Voices in the park

What had been a boring, grey wall was now re-painted into bright, reddish colours. 

What were bare, lifeless trees were now steady, glowing, white trees.

What had been a poor Santa begging for money to support his wife and millions of kids was now a spectacular, joyful dancer!

What had been ordinary dull flats had become different coloured, shaped windows such as red hearts and  yellow squares.
What had been old, abandoned portraits of the Mona Lisa and a Cavalier sitting on tiny floods of water, all sad were now a beautiful Mona Lisa prancing happily with the Cavalier!
All sad things become ecstatic and exultant things!

Voices in the Park

What had been a grey, plain  lamppost was now an exotic ,white flower lamppost. What had been a boring, mucky wall was now a colourful red and yellow wall. What had been a dreary block of black flats was now a lit up beautiful set of apartments. What had been a bent, naked tree was now a straight tree full of Christmas lights. What had been a grey, dirty street was now a clean, shiny road. Where there had been a grey, long fence there was now no fence. What had been a sitting Santa begging for money was now a happy ballet dancer.

Voices in the park: Differences

Before the buildings looked abandoned - they were dark and lonely but now there is life and the different-shaped windows are full of light and colour. King Kong now stands on the roof of one of the buildings.  What were trees that looked old and weak are now full of energy, with glorious trunks and well-shaped branches. There are no leaves still, but I guess it's just not the season. I'm sure they'll grow when it's time. What was a boring old lamppost, now is an exotic flower which lets out a warm, mystical light. Before, the wall colours were pale and dirt was all over the place, but now it's been painted and cleaned. Notice this little detail: There's a heart in the left-down corner. To begin with it was transparent and broken into 2 pieces. Now it's unified and painted a bright red colour. Before, there were sad paintings leaning on the wall. Now, they have come to life and are kissing. Santa-beggar who was sitting by the wall, is now transformed into a Santa-ballerina! Clearly, before it was the street of sadness, and now it's the street of delight!

Voices in the Park

He had been miserable and bored but now he was happy and glad. Santa had been begging for money but now he was rich and dancing like a ballerina. What had been a broken grey heart was now a beautiful red heart. An ordinary lamp post was now a fairy-white precious flower post. Two  portraits were sad and dull but now  the portraits have come alive!

Voices in the Park

The street was a dark, unhappy place, until one magical night came and changed everything.  What had been a boring red sky with a city full of rubbish below it became full of stars and a precious dark colour with no more rubbish on the ground. Where there had been a poor Santa supporting his wife and millions of kids there was no more poor Santa he was now dancing.  He was the Santa Claus jumping about enjoying the night.  What had been paintings that were always sad and would never smile suddenly just came to life and started dancing very romantically with a real big smile. This boring sadness would never happen again.

Voices in the Park

He was sad and feeling down but then he was good and happy because Smudge had made jokes. What had been a wall that was old but strong with a fence on top had become a brighter wall, with no fence and it was more welcoming. What had been a dull and sad area was now cheerful and colourful. What had been an empty building had become a more lively building with windows of different shapes and colours and had a super hero on top. What had been Santa beggar had changed into a dancing ballerina. Before the pavement was broken and cracked but now it was smooth and clean. Where there was no life in the tree it is now full of fire flies everywhere.

Voices in the Park

What had been a Santa begging on the street was now a happy fellow.
What had been a dirty street was now a clean street.
What had been two ordinary paintings sitting by the wall had transformed into lovely dancers.
The old boring trees had became strong trees with life.
A broken lamppost was a new looking lamppost.
Dark walls were now bright with colour.

Voices in the Park

What had been an old, dark lamp post had turned into a bright, flower lamp post.  What had been an empty heart without love and colour turned red like blood.  He had been lonely and sad but now he was filled with happiness.
What had been a stinky road turned into a clean streets.

The letter K comes from the Greek letter Κ (kappa), which was taken from the Phoenician  kap, the symbol for an open hand.

This, in turn came Egypt from the hieroglyph for hand. The first people to make an alphabet made it a K because their word for hand started with that sound.

In the earliest Latin inscriptions, the letters C, K and Q were all used to represent the sounds /k/ and /g/ (which were not differentiated in writing).

the forth letter K was from paleo-Hebrew:

The last letter K was from Greek:

Voices in the Park

What had been dull, beige walls were now bright yellow walls.
What had been a boring, ordinary lamp post, was now a lamp post shaped like an exotic, beautiful flower. What had been a poor Santa beggar was now a cheerful dancing spirit. What had been a sad Mona Lisa on a flat canvas painting was now dancing.
What had been grey dirty flats, was now a bright, colourful appartment with shapes for windows.
What had been a disgusting, old street with rubbish all over (and   there was even a rat) was now a clean shiny road.
What had been a horrible, broken heart, was now a bright red heart.

Voices in the Park

When going to the park he was dismal, and now he was joyful like a jolly Father Christmas. What had been an old and dirty city, was now a clean and modern city. There stood an old lamp post near the lonely street that had become a bright and cheerful lamp post next to the joyful dancing people. Where once the portraits had been abandoned in the dirty road there were now dancing people.

Voices in the park

What were once old, boring flats were now beautiful apartments with colourful shaped windows. What had been Father Christmas begging for money was now Father Christmas dancing happily like a ballerina. What had been sad paintings were now dancing alive people. Before the street was all full of rubbish with rats running around and was now really clean.

Letter T

                                      T

The letter T started by an X back in the ancient EGIPTIANS times.

Then it turned into the sign of a cross in the ancient PROTO-SINAITIC like this

Next it came back into an X back into the PHOENICIAN

 

After a while in the ancient GREEKS it turned  into a bird footprint

 

 

It evolved into a type of N in the ancient ARMAIC times

 

Then it turned almost into our T in the ROMAN times

Next it turned into our T MODERN UROPEAN.

 

 

 

Voices in the Park

He had been very sad on a damp, lonely street and now he was happy. What had been a poor beggar dressed up as Santa Claus was now a Santa Claus ballet dancer.  What had been sad, old paintings of the Mona Lisa were now a romantic couple dancing joyfully near the bright colour wall. Instead of a breaking heart there was a little reddish heart painted on the wall. What had been a lonely grey lamp was now a beautiful flowery shiny lamp. What had been dull black apartments were now full of multi-coloured windows with King Kong on the top! What had been some ugly annonimous footprints where now a set of white little footprints from Dad and his little girl, Smudge!

Voices in the Park

The man was very bored but now he was very joyful. What had been a damp, old lamppost was now a beautiful lit-up flower. What had been two dark paintings were now two people dancing. What had been a Santa-beggar had become a Santa-dancer. What had been a broken building was now a nice building with colourful lights and a superhero on top! What had been a stinky street became now a polished street with no rubbish. What had been a sad man walking on one side became a happy man walking the other way. What had been a damp sky became a sky with lots of stars and a shooting star! What had been a black broken heart became a heart red like blood!

K

The letter K back when the Egyptians were learning about the alphabet.
They used think if we have a thing we can make it into something called a letter. The K used to look like this the Proto-Sinaitic.

For the Egyptians this was "kaf", the palm of a hand:

It became K.

It's quite odd. I know that, but that's what it looked like back in time. The letter K has evolved into something similar to our letter K.

This was the Phoenician K:

It's odd as well, its like its on its head jumping. 

And then finally the Greeks have changed it into this K. 

the letter o and its story

       o

THIS IS THE LETTER O WHICH WE USE TODAY.

This was the letter o which they used in the ancient Egyptian! It meant an eye, and they said it "en".

 

This was the letter o which the Proto -Sinaitic used to write in the first alphabet:

This was the letter o which the Phoenicians used to write!

This was the letter o which the Greeks used to write!

This was the letter o which the Etruscans used to write!

This is now the letter O that we use: